Topologia Geral
Conexidade e compacidade
Espaços conexos
A definição usual de conexidade se dá em torno de separações ou cisões. Uma cisão de um espaço topológico é uma partição do espaço cujas componentes são abertos. O espaço é dito conexo se a sua única cisão é a trivial. Intuitivamente, por ser aberta, cada componente de uma cisão já carrega consigo todos os pontos próximos
de si mesma. Assim, a existência de uma cisão não trivial corresponde a um espaço com mais de uma região que contém todos os seus pontos próximos
.
Fecho de conexo é conexo
De fato, se E \subseteq X é conexo, todo E \subseteq F \subseteq \closure{E} é conexo também.
Seja \{A, B\} uma cisão de F. Como E é conexo, então E \subseteq A ou E \subseteq B. Em ambos os casos, A e B são fechados em \closure{E}, que é fechado em X, logo são fechados em X. Daí, \closure{E} \subseteq A ou \closure{E} \subseteq B, de onde segue que a cisão é trivial.
Espaços compactos
Um espaço topológico é dito compacto se toda cobertura de X possuir subcobertura finita.
Subespaços
Um subespaço de um espaço topológico compacto é compacto se, e somente se, ele for fechado.
Exercícios
Munkres 1, 2, 5, 7, 8, 10, 12
-
Questões gerais
-
Sejam \tau' \supseteq \tau duas topologias em X. O que a compacidade de X em uma dessas topologias implica sobre a compacidade na outra?
Se \tau' for compacto, então \tau também é. A outra implicação não é verdadeira: por exemplo, a topologia trivial em um espaço não compacto é compacta.
-
Mostre que se X é compacto roam:Hausdorff sob ambas \tau e \tau', então ou \tau = \tau' ou elas não são comparáveis.
É suficiente mostrar que \tau \subseteq \tau' \implies \tau = \tau'. Suponha \tau \subseteq \tau', e vamos mostrar a outra inclusão. Seja U \in \tau'. Como U^{\complement} é fechado, é compacto em \tau'. Mas vimos acima que isso implica em U^{\complement} ser compacto em \tau, que é Hausdorff, logo U^{\complement} é um fechado de \tau. Isso mostra que U \in \tau.
-
-
Reais
- Ok
- Não: seja S = [0,1] ∖ \QQ, e \mathcal{U} = \{ S \cup \{q\} : q \in \QQ \}.
- Para cada ponto x \in A, conseguimos uma vizinhança V_x de x que é disjunta de um aberto U_x \supset B. Fazemos a cobertura de A por esses abertos, e extraímos uma subcobertura finita. A subcobertura V_{x_1} \cup \dots \cup V_{x_N} resultante e a interseção U_{x_1} \cap \dots \cap U_{x_N} são os abertos desejados.
- Seja C \subseteq X \times Y um fechado. Tome x \in X ∖ \pi(C). Sabemos que x \times Y \subseteq C^{\complement}, logo pelo Lema do Tubo existe uma vizinhança W de x tal que W \times Y \subseteq C^{\complement}. Assim, (w,y) \notin C para todo w \in W, y \in Y, ou seja, w \notin \pi(C). Isso mostra que x \in W \in X \setminus \pi(C), logo \pi(C) é fechado.
- Suponha f contínua. Seja \equiv : Y \times Y \to \{0,1\} o mapa Então G_f = ((x,y) \mapsto (f(x) \equiv y))^{-1}(0)
Subespaços compactos da reta
Teorema dos Extremos (Weierstrass)
Seja f \colon X \to Y contínua, onde Y é um conjunto com a topologia da ordem e X é compacto. Então existem pontos c e d de X tais que f(c) \leq f(x) \leq f(d) para todo x \in X.
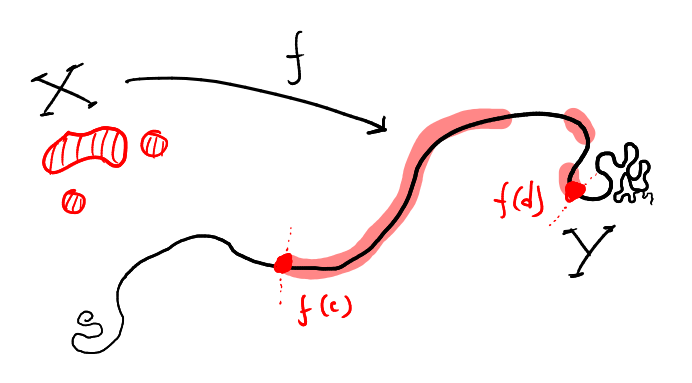
A imagem f(X) é compacta, portanto basta mostrar que f(X) possui maior e menor elementos. Se não fosse o caso, por exemplo, de haver maior elemento, então a coleção \{(-\infty, a) : a \in A\} seria uma cobertura de f(X), que possui subcobertura finita \{(-\infty,a_1),\dots,(-\infty,a_N)\}. Mas isso significa que \max \{ a_1,\dots,a_N \} \notin A, absurdo.
Número de Lebesgue de uma cobertura
Seja \mathcal{A} uma cobertura aberta do espaço métrico (X,d). Se X for compacto, existe \delta > 0 tal que todo subconjunto de X com diâmetro menor que \delta está contido em um elemento de \mathcal{A}. \delta é dito um número de Lebesgue para \mathcal{A}.
Compacto Hausdorff sem pontos isolados é não enumerável
Seja X espaço Hausdorff compacto sem pontos isolados. E
Corolário óbvio: compacto Hausdorff com um ponto não isolado é não enumerável.
Exercícios
- Simples.
- Fixando qualquer ponto x \in X, basta observar que a imagem S = d(x,X) \subseteq \RR é um subconjunto enumerável. Tomando algum r \in (\inf S, \sup S), é imediato que a bola B(x,r) = B[x,r] é fechada, aberta e diferente de X.
- TODO
-
Sobre o conjunto de Cantor
- Totalmente desconexo: pois não contém nenhum intervalo.
- Compacto: pois é fechado e limitado
- booo
- Basta observar que tem uma sequência de extremos convergindo para qualquer ponto do Cantor.
- Aplicando Compacto Hausdorff sem pontos isolados é não enumerável, obtemos o que foi desejado. (embora existam formas mais diretas).
Compacidade de ponto limite (sequencial)
É uma noção de compacidade mais fraca, mas que coincide com a noção usual em espaços métricos:
Um espaço topológico X é dito ponto de acumulação compacto se todo subconjunto infinito possuir ponto limite.
Compacto ⇒ ponto de acumulação compacto
Se X é compacto e Q é um subconjunto infinito. Se Q não tem ponto limite, então \bar{Q} = Q, logo Q também é compacto. Além disso, todo x \in Q não é ponto limite de Q, logo tem uma vizinhança V_x sem outros pontos de Q. Temos Q = \bigcup_{x \in Q}V_x, de forma que existe subcobertura Q = V_{x_1} \cup \dots \cup V_{x_n} = \{x_1,\dots,x_n\}, impossível já que Q é infinito.
Exercícios
-
Seja [0,1]^{\omega} na topologia uniforme. Encontre um subconjunto infinito desse espaço que não possui ponto limite.
Simples: basta tomar X = \{ (\underbrace{0,\dots,0,1}_{n \text{ entradas}},0,\dots) \mid n \in \NN\}.
-
Mostre que [0,1] não é ponto de acumulação compacto como um subespaço de \RR_l.
Seja x_n = 1 - 1/n, que é um conjunto enumerável de pontos distintos. Como x_n só possui 1 como ponto de acumulação na topologia usual da reta, e a topologia do limite inferior é mais fina que a topologia usual, sabemos que x_n não pode possuir outros pontos limite além do 1 em \RR_l. De fato, 1 não é um ponto limite, pois [1,2) \ni 1 é uma vizinhança de 1 que não contém nenhum ponto de x_n.
-
Um espaço X é dito enumeravelmente compacto se toda cobertura contável possui uma subcobertura finita. Mostre que para um espaço T_1, compacidade enumerável é equivalente a compacidade ponto-limite.
Demonstração.Se X for enumeravelmente compacto, tome Q = \{x_n\}_{n \in \NN} um subconjunto infinito. Se Q' = \emptyset, então de \bar{Q} = Q \cup Q', temos \bar{Q} = Q. Logo, Q seria subespaço fechado, portanto enumeravelmente compacto. Como um conjunto sem pontos limite é discreto, todo ponto de Q é aberto em Q. Logo o conjunto de pontos de Q forma uma cobertura enumerável de Q, que possuiria subcobertura finita, absurdo.
Reciprocamente, suponha Q é ponto de acumulação compacto, e \{U_n\} uma cobertura enumerável. Seja W_n = U_1 \cup \dots \cup U_n. Se não houver subcobertura finita, então para cada n, existe x_n, x_n \notin W_n. Além disso, por construção existe m \geq n tal que x_n \in W_m, logo \{x_n\}_n é um conjunto infinito, portanto possui algum ponto limite x. Mas esse ponto não pode estar em nenhum U_n, pois se estivesse, U_n seria uma vizinhança de x, logo pelo fato do espaço ser T_1 existiria m \geq n tal que x_m \in U_n, absurdo já que x_m \notin U_n para m \geq n.
-
Seja (X,d) um espaço métrico. Mostre que se f : X \to X for uma isometria e X for compacto, então f é bijetiva e portanto é um homeomorfismo.
Queremos mostrar que f é sobrejetora (já que uma isometria é obviamente injetiva). Suponha que exista a_0 \in f(X)^{\complement}. Como f(X) é compacto, \varepsilon = d(a_0,f(X)) > 0. Em particular, d(a_0,f(a_0)) \geq \varepsilon, logo por f ser isometria, d(f^n(a_0),f^{n + 1}(a_0)) \geq \varepsilon.